Diffusion models have quickly risen in popularity for their ability to model complex distributions and perform effective posterior sampling. Unfortunately, the iterative nature of these generative models makes them computationally expensive and unsuitable for real-time sequential inverse problems such as ultrasound imaging. Considering the strong temporal structure across sequences of frames, we propose a novel approach that models the transition dynamics to improve the efficiency of sequential diffusion posterior sampling in conditional image synthesis. Through modeling sequence data using a video vision transformer (ViViT) transition model based on previous diffusion outputs, we can initialize the reverse diffusion trajectory at a lower noise scale, greatly reducing the number of iterations required for convergence. We demonstrate the effectiveness of our approach on a real-world dataset of high frame rate cardiac ultrasound images and show that it achieves the same performance as a full diffusion trajectory while accelerating inference 25×, enabling real-time posterior sampling. Furthermore, we show that the addition of a transition model improves the PSNR up to 8% in cases with severe motion. Our method opens up new possibilities for real-time applications of diffusion models in imaging and other domains requiring real-time inference.
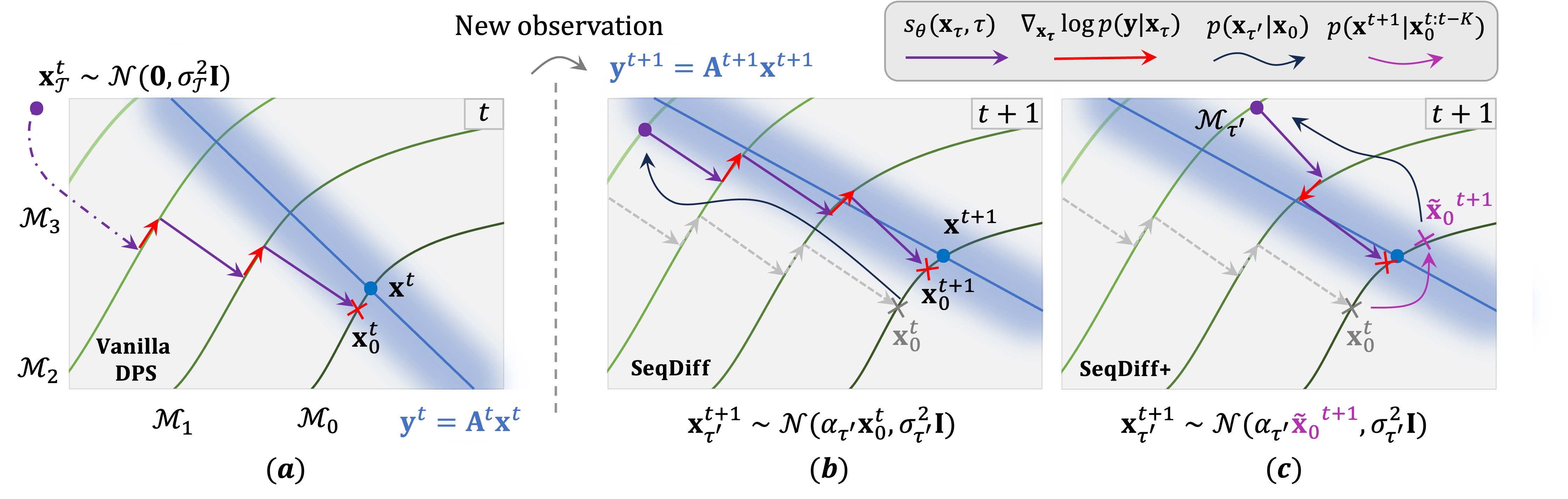Geometric representation of the reverse diffusion process and corresponding manifolds $\mathcal{M_\tau}$ for each diffusion timestep $\tau$. In $\textbf{(a)}$ a standard conditional reverse diffusion trajectory starting from a Gaussian sample $\mathbf{x}_\mathcal{T}\sim\mathcal{N}$ is shown with DPS as guidance rule. For initialization of the next frame $t+1$, we propose two different methods SeqDiff and SeqDiff+, depicted in $\textbf{(b)}$ and $\textbf{(c)}$ respectively. In the first option we initialize the trajectory from a noised version of the Tweedie estimate of the previous frame, $p(\mathbf{x}_{\tau^\prime}^{t+1}|\mathbf{x}_0^{t})$ with $\tau^\prime \ll \mathcal{T}$. The second option improves upon this by predicting the next frame with $\tilde{\mathbf{x}}_0^{t+1} \approx f(\cdot)$, accounting for any motion between frames. This leads to the initialization $p(\mathbf{x}_{\tau^\prime}^{t+1}|\tilde{\mathbf{x}}_0^{t+1})$, with $\tau^\prime_{\text{SeqDiff+}} < \tau^\prime_{\text{SeqDiff}}$.