Solving ill-posed inverse problems requires careful formulation of prior beliefs over the signals of interest and an accurate description of their manifestation into noisy measurements. Handcrafted signal priors based on e.g. sparsity are increasingly replaced by data-driven deep generative models, and several groups have recently shown that state-of-the-art score-based diffusion models yield particularly strong performance and flexibility. In this paper, we show that the powerful paradigm of posterior sampling with diffusion models can be extended to include rich, structured, noise models. To that end, we propose a joint conditional reverse diffusion process with learned scores for the noise and signal-generating distribution. We demonstrate strong performance gains across various inverse problems with structured noise, outperforming competitive baselines that use normalizing flows and adversarial networks. This opens up new opportunities and relevant practical applications of diffusion modeling for inverse problems in the context of non-Gaussian measurement models.
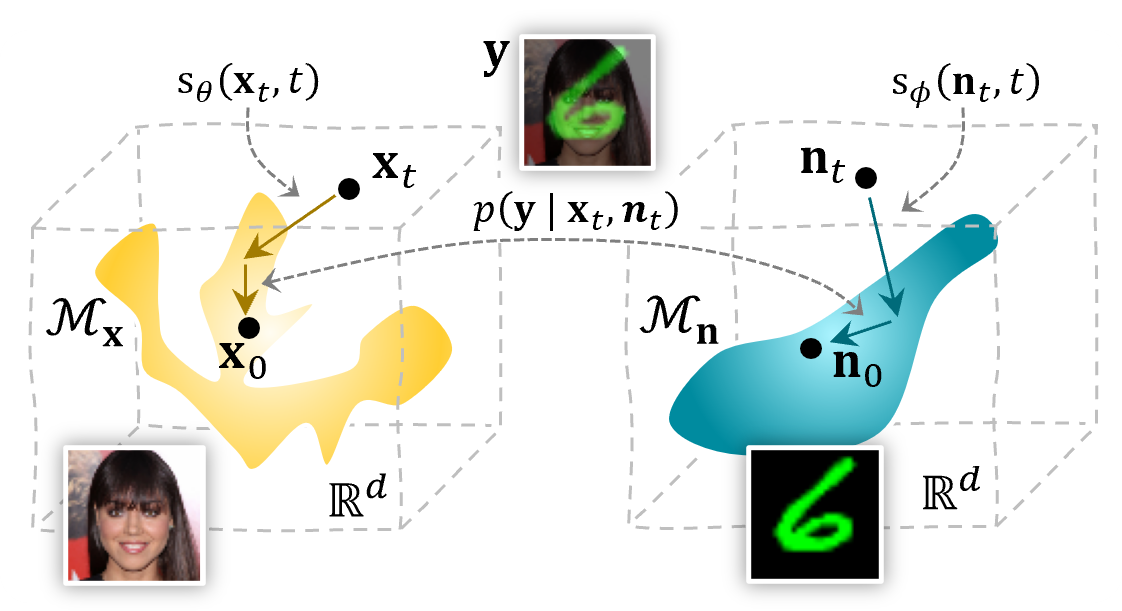
Overview of the proposed joint posterior sampling method for removing structured noise using diffusion models.